by Dr. Dimitrios Karanikolopoulos, Foundation for Research and Technology-Hellas
The Ising model offers an effective framework for addressing NP-hard combinatorial optimization problems, as many of these problems can be reformulated via finding the ground state of the Ising Hamiltonian. However, as the size of the problem increases, the computational demand for simulating Ising spin dynamics grows exponentially. Photonic Ising machines have demonstrated substantial potential in solving large-scale combinatorial optimization problems. As a novel computational architecture, the photonic Ising machine is expected to achieve several orders of magnitude faster computational speeds compared to its electronic counterparts.
Recently, a spatial photonic Ising machine (SPIM) based on spatial optical modulation has been introduced by the SAP team of the HEISINGBERG project [1]. In this system, the spin information of the Ising model is spatially encoded onto the wavefront of the light field using a programmable spatial light modulator (SLM), taking full advantage of the spatial light field’s parallelism. This design enables the simulation of tens of thousands of fully connected Ising spins. Nonetheless, the analog nature of the SPIM limits its computational accuracy, particularly as the number of spins increases, thereby restricting its practical applicability in solving large-scale problems.
Under optimal conditions, the SPIM can simulate the interaction strength between spins in the Ising model by modulating the phase distribution of the incident light’s wavefront. The discrete Ising spin information is encoded onto the SLM, and after being Fourier transformed by imaging with a lens, the light intensity at the central position of the back focal plane corresponds to the Ising model Hamiltonian. However, in real-world optical systems, aberrations are unavoidable. These wavefront distortions lead to deviations in the actual light propagation from the ideal Fourier transformation, ultimately degrading the computational accuracy of the SPIM.
In preparation for executing optical experiments which involve addressing the phase front of laser beams using SLMs it is essential to consider a number of technical issues pertaining to such systems. Although modern SLMs offer phase manipulation of the incident laser beam in a wide range of values, all hardware currently available suffers to a lesser or greater extend from three problems of technical nature, namely, curvature of the LCOS display, non-linear phase response and pixel crosstalk effects [2, 3]. The first two problems are mitigated by using correction phase masks to negate the curvature effect and specific look up tables both of which are either provided by the manufacturer or can be measured. The crosstalk effect has plagued holography applications the last few decades with viable solutions to the problem only recently having been brought forth [4, 5, 6].
Having addressed the above hardware related drawbacks, the intricate problem of accurately measuring the phase variations of the laser wavefront presents itself as the main source of error. As the beam propagates throughout the optical system, transmission/reflection from imperfect non-flat optical elements will introduce distortions to the laser profile.
Within the HEISINGBERG project, the FORTH team has developed a method to optimize the operation of a SPIM by extending the spin scale through compensation of optical aberrations. This requires compensation of the light wavefront illuminating the SLM and is achieved by retrieval the phase of the incident field and the creation a suitable mask which is subsequently loaded on the SLM to negate the aberration effects. Experiments and simulations demonstrate that the optimization of the SPIM leads to increased detection efficiency resulting in substantial improvement in computational accuracy.
As the phase retrieval method of choice, we have opted for the method introduced in [7] which offers a robust and straightforward way to recover the phase over the SLM display by retrieving it via sinusoidal fitting of 2D interferograms recorded by sampling the LCOS display with square tiles of blazed gratings [5]. This method offers a direct probe into the phase profile at the SLM plane which can be subsequently used to compensate for any imperfections with excellent accuracy in the order of λ/40 [7].
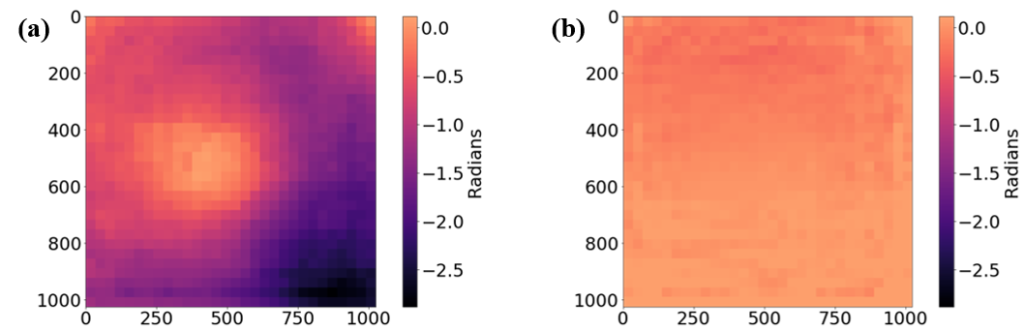
Phase retrieval and correction. (a) Relative phase, δφ, obtained through the phase retrieval algorithm at the SLM plane (b) Resulting phase after applying the correction phase mask created from measurement (a) [data obtained by Panagiotis Karavelas].
References
- D. Pierangeli, G. Marcucci, and C. Conti. Large-scale photonic Ising machine by spatial light modulation. Phys. Rev. Lett. 122, 213902 (2019).
- Holoeye Spatial Light Modulators Application Note: https://holoeye.com/wp-content/uploads/Application_Note_SLM-V.60.pdf
- M. Carbonell-Leal and O. Mendoza-Yero. Encoding complex fields by using a phase-only optical element: mitigation of pixel crosstalk effects. Optica Open. (2019).
- O. Mendoza-Yero, G. Mínguez-Vega, and J. Lancis, Encoding complex fields by using a phase-only optical element. Opt. Lett. 39, 1740-1743 (2014).
- P. Schroff, A. La Rooij, E. Haller, et al. Accurate holographic light potentials using pixel crosstalk modelling. Sci. Rep. 13, 3252 (2023).
- P. Schroff, E. Haller, S. Kuhr, and A. La Rooij, Rapid stochastic spatial light modulator calibration and pixel crosstalk optimization, Opt. Express 32, 48957-48971 (2024).
- P. Zupancic, P. M. Preiss, R. Ma, A. Lukin, M. E. Tai, M. Rispoli, R. Islam, and M. Greiner. Ultra-precise holographic beam shaping for microscopic quantum control, Opt. Express 24, 13881-13893 (2016).
